최신연구
[안희갑 교수] Minimum Convex Hull and Maximum Overlap of Two Convex Polytopes
[연구의 필요성]
형태 매칭 문제는 알고리즘 분야에서 근본적인 문제로, 이미지 처리, 컴퓨터 비전, 머신 러닝 등 다양한 컴퓨터 관련 분야에서 널리 활용된다. 두 물체의 유사성을 측정하는 방법으로는 두 물체의 볼록 헐 최소영역이나 두 물체의 겹침 최대영역을 계산하는 방식이 있다. 특히, 2차원에서 두 물체의 볼록 헐 최소영역을 구하는 알고리즘은 O(n log n) 시간 복잡도를 가지며, 2012년에 해당 알고리즘이 발표되었다. 이 이후로 개선된 알고리즘이 존재하지 않았고, 이 문제를 해결하는 최적의 알고리즘을 개발하는 것은 여전히 큰 난제이다.
[포스텍이 가진 고유의 기술]
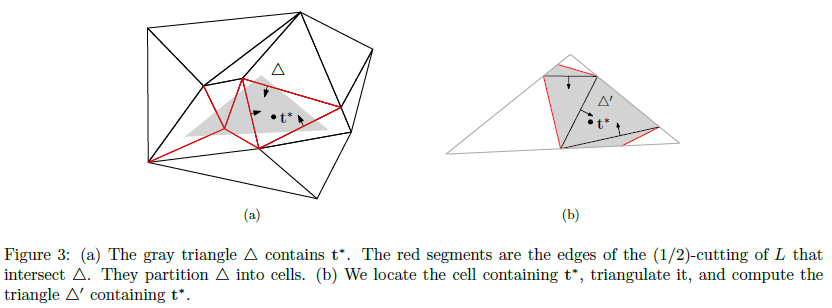
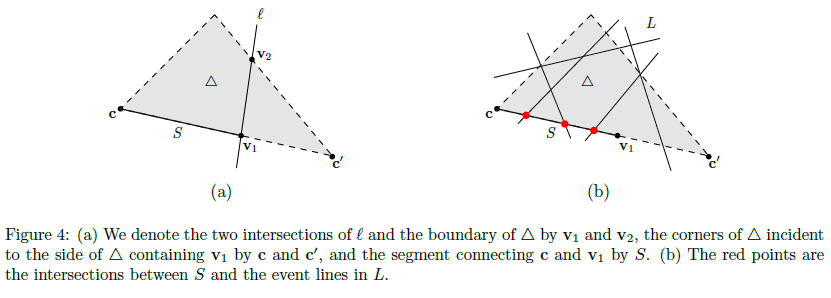
본 기술의 핵심 아이디어는 면적 함수 상에서 주어진 선과 최적의 점의 위치 관계를 효율적으로 구하는 알고리즘을 개발한 것이다. 이를 위해 먼저 면적 함수를 선으로 제한했을 때 최적의 점을 구하는 알고리즘을 활용하여 위치 관계를 구할 수 있음을 증명했다. 그리고 기존에 계산된 값을 바탕으로 두 물체의 볼록 헐 영역을 직접 구하지 않고, 선 위의 최적 점을 구하는 알고리즘을 개발했다. 이를 통해 두 물체의 꼭짓점 개수와 무관한 시간 복잡도를 갖는 알고리즘을 도출할 수 있었다. 마지막으로, 위의 방법과 cutting algorithm을 재귀적으로 적용하여 최적의 알고리즘을 완성했다.
[연구의 의미]
본 연구는 알고리즘 분야에서 50년 이상 미해결된 난제를 해결한 중요한 연구이다. 이 기술은 고차원으로의 확장이 가능하며, 최대 겹침 문제에도 적용할 수 있어 다양한 문제에 응용이 가능하다.
[연구결과의 진행 상태 및 향후 계획]
본 연구 결과로 2차원 볼록 헐 최소화 문제에 대한 최적 알고리즘을 제시했다. 또한, 고차원 및 다양한 문제들에 대해서도 기존 결과들의 시간 복잡도를 상당히 개선했다. 본 논문에 제시된 알고리즘을 통해, 강체 운동 조건 하에서의 문제를 해결하는 정확한 알고리즘을 개발할 수 있을 것으로 기대된다.
[성과와 관련된 실적]
Mook Kwon Jung, Seokyun Kang, Hee-Kap Ahn. Minimum Convex Hull and Maximum Overlap of Two Convex Polytopes. 36th ACM-SIAM Symposium on Discrete Algorithms (SODA 2025)
[성과와 관련된 이미지]