최신연구
[김동우 교수] Mitigating Oversmoothing Through Reverse Process of GNNs for Heterophilic Graphs
[연구의 필요성]
기존에 제안된 그래프 신경망은 이웃한 정점들끼리 동일한 분류에 속할 가능성이 높은 동종애(homophilic) 그래프에 적용될 때는 높은 성능을 보이지만, 이웃한 노드들끼리 다른 분류에 속할 가능성이 높은 이종친화적(heterophilic) 그래프에서는 낮은 성능을 보인다. 이종친화적인(heterophilic) 특징을 가지는 그래프에서는 멀리 떨어져 있는 정점들과의 관계를 잘 학습하는 것이 중요해 깊은 그래프 신경망을 이용해야 하는데, “oversmoothing” 문제로 인해 신경망을 깊이 쌓기가 어렵기 때문이다. “oversmoothing” 문제란, 그래프 신경망을 깊게 쌓을 수록, 출력되는 각 정점들의 특징값(node representation)이 유사해져서, 서로 구분하기 어려워지는 문제를 가리킨다. Oversmoothing 문제에 대해서 기존 연구는, 그래프 신경망을 통한 정점의 특징값 학습 과정이 열 확산 과정과 본질적으로 동일한 형태를 가지고 있어 피하기 어려운 문제라고 지적하기도 했다. 이러한 문제로 인해, 여전히 그래프 신경망을 통해 이종친화적(heterophilic) 그래프의 정점을 분류하는 것은 어려운 문제이다.
[포스텍이 가진 고유의 기술]
본 연구에서는 기존의 그래프 신경망의 역과정을 활용해 이종친화적(heterophilic) 그래프의 정점 분류 성능을 향상시켰다. 긴 쇠막대기의 한쪽 끝을 불에 달구면, 처음에는 반대쪽 끝편은 뜨겁지 않다. 하지만 시간이 지나면 열이 확산되어 반대쪽 끝편도 뜨거워진다. 이처럼, 열은 시간이 지날수록 퍼져나가 평형 상태에 도달한다. 기존의 그래프 신경망을 쌓는 것은 정점의 특징값 정보가 열처럼 다른 정점들로 퍼져나가도록 해서, 깊게 쌓으면 열의 평형상태와 같이 모든 정점의 특징값이 비슷해지도록 만들었다. 역과정을 활용하는 것은, 열이 확산되기 전에 좁은 구역에 집중되어 있어 다른 구역들과 차이가 두드러지는 시점으로 시간을 거슬러 올라가는 것이다. 즉, 본 연구에서 제안한 역과정 그래프 신경망을 쌓으면, 구조망을 통과하는 정점들 사이의 특징값의 차이가 두드러지는 결과물을 출력할 수 있다. [그림1]은 역과정이 가지는 효과를 직관적으로 설명하기 위한 예시이다. 본 연구에서는 기존에 제안된 세 개의 신경구조망 구조, GRAND, GCN, GAT에 대한 역과정을 구현하는 방식을 제안하였다. 구현한 구조를 실제 데이터에 적용한 결과를 시각화하여 나타낸 것이 [그림2]이다.
[연구의 의미]
제안된 그래프 신경망의 역과정은 oversmoothing 문제를 완화한다. oversmoothing 문제는 그래프 신경망을 깊게 쌓지 못하게 하여, 표현력을 제한하고 멀리 떨어진 정점과의 관계를 보는 것을 방해하였다. 본 연구에서 제안하는 방법은 oversmoothing 문제를 해결하는 새로운 방법을 제시한다. 또한, 기존에 oversmoothing 문제로 인해 해결이 어렵던 문제 중 하나인 이종친화적(heterophilic) 그래프에서의 정점 분류 문제의 성능을 높였다.
[연구결과의 진행 상태 및 향후 계획]
제안된 방법은 이종친화적(heterophilic) 그래프 데이터에서 기존의 방법에 비해 좋은 성능을 보인다. 하지만 역과정을 구현하기 위해서는 기존의 그래프 신경망이 특정 조건을 만족하도록 제한을 두어야 한다. 이것은 그래프 신경망의 표현력을 제한해 성능 향상 폭을 낮출 수 있다. 때문에, 좀 더 낮은 수준의 제한으로 역과정을 구현할 수 있는 방법을 찾아 성능을 더 향상시킬 계획이다.
[성과와 관련된 실적]
MoonJeong Park, Jaeseung Heo, Dongwoo Kim, “Mitigating Oversmoothing Through Reverse Process of GNNs for Heterophilic Graphs”, 2024 International Conference on Machine Learning (ICML)
[성과와 관련된 이미지]
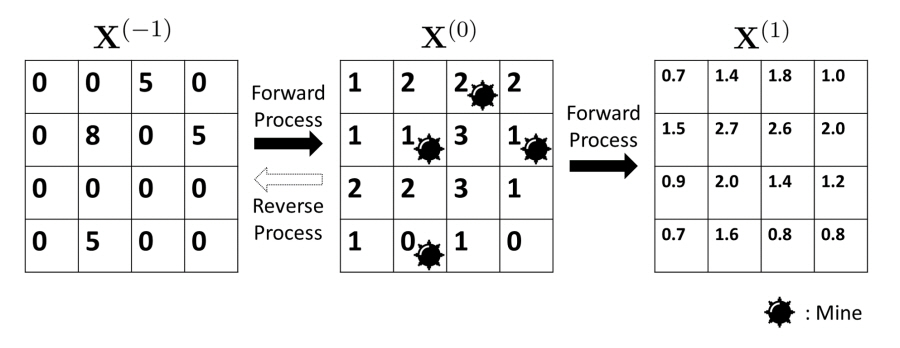
[그림1] 주어진 예시는 지뢰찾기 문제로, 격자 그래프 X(0)로부터 모든 지뢰를 찾는 것을 목표로 한다. 각각의 격자는 그래프의 정점을 나타내며, 각 정점은 대각선 방향을 포함한 여덟개의 인접한 정점들과 연결되어 있다. X(0) 상황에서 각 격자마다 주어진 숫자는, 이웃 정점 중 지뢰인 정점의 개수를 나타낸다. 인접행렬 A와 차수행렬 D를 이용하면, X(k+1) = AD-1X(k)과 같이 그림의 순과정을 나타낼 수 있다. 역과정을 통해 얻은 X(-1)에서는, 5보다 큰 값을 가지는 정점을 선택함으로써 지뢰를 100%의 정확도로 찾아낼 수 있지만, 순과정을 통해 얻은 X(1)에서는 지뢰를 찾는 정확도가 50%로 떨어진다.

[그림2] 실제 “지뢰찾기” 데이터에서 순과정과 역과정이 일어날 때 각 정점이 가지는 특징값의 변화를 시각화한 이미지이다. 상단의 이미지는 순과정과 역과정 모두를 사용하는, 본 연구에서 제안한 방법을 사용했을 때의 이미지이고, 하단의 이미지는 순과정만을 사용한 기존의 방법론을 사용했을 때의 이미지이다. 처음에 주어진 X(0)에서의 정점 특징값은 순과정이 진행될수록 다른 정정의 특징값들과 비슷해진다. 반면 역과정이 진행되는 경우에는, 정점의 특징값의 차이가 더 두드러진다.

